K Means Clustering in Python

In this tutorial we would learning how to implement K - Means Clustering in Python along with learning how to form business insights..

To learn about K-means in detail you can refer the following article: K Means Clustering

For this tutorial we will make use of the following dataset. Click below to download the following:

KMeans_data

.csv

Download CSV • 128KB

Firstly let us load pandas in our environment

import pandas as pd

Let us read our CSV file

X = pd.read_csv("Kmeans_data.csv")

Now we are viewing initial rows of our dataset. It is a retail dataset where each row represents different customer. We have the following columns:

• CustomerID: Unique identifier for each customer

• Amount: Total monetary value of the transactions till today by a customer

• Frequency: How many times a customer has come to our store

• Recency: How many days ago the customer came to our store

X.head()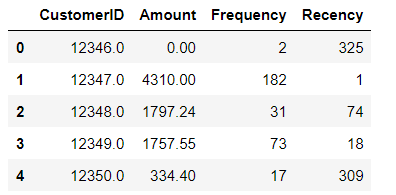

Let us look at the shape of our dataset. We have 4293 rows and 4 columns

X.shape

Output: (4293, 4)

Let us load all the other libraries for this lesson:

from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans

The variables in our data has different scales (eg., amount is in 100s to 1000s, while recency and frequency column have values less than 1000). thus it might adversely impact the calculation of Euclidean distance calculated while running K-Means clustering. Due to this we need to standardise our data to have the same scale.

Initialising the standard scaler:

scaler = StandardScaler()

Fitting and storing our scaled data in X_scaled.

X_scaled = scaler.fit_transform(X)

Our scaled array looks as follows:

X_scaled

Output:

array([[-1.71465075, -0.72373821, -0.75288754,  2.30161144],
       [-1.71407028,  1.73161722,  1.04246665, -0.90646561],
       [-1.71348981,  0.30012791, -0.46363604, -0.18365813],
       ...,
       [ 1.73043864, -0.67769602, -0.70301659,  0.86589794],
       [ 1.73101911, -0.6231313 , -0.64317145, -0.84705678],
       [ 1.73392146,  0.32293822, -0.07464263, -0.50050524]])

Let us run K-means with some arbitrary k = 3.

To run K-means with 3 clusters we use KMeans function.

n_clusters specifies the number of clusters.

max_iter denotes the maximum number of iterations in K-means. For similicity we are using 50 iterations.

kmeans = KMeans(n_clusters=3, max_iter=50)

#Fitting K-means on our scaled data
kmeans.fit(X_scaled)

The following code provides us the cluster labels for our data: It denotes that 1st observation belongs to cluster 0, 2nd observation belongs to cluster 2, etc.,

kmeans.labels_

Output: array([0, 2, 1, ..., 0, 1, 1])

Finding the Optimal Number of Clusters

Since K-means requires the value of 'k' to be pre-defined thus we had build K-means algorithm by arbitrarily taking k=3, but it might not be the optimal value for 'k'. To find the optimal number of clusters for K-means we are using elbow curve. The Elbow Method is one of the most popular methods to determine this optimal value of k.

For this we are taking number of clusters from 2 to 14, and building a K-means model to each one of them.

inertia_ returns the 'cost function' or distortion for K-means.

Thus for each value of 'k' we are saving this distortion in an array SSE.

ssd = []
range_n_clusters = range(2,15)
for num_clusters in range_n_clusters:
    kmeans = KMeans(n_clusters=num_clusters, max_iter=50)
    kmeans.fit(X_scaled)
    
    ssd.append(kmeans.inertia_)

Now we are plotting our SSE with respect to number of clusters:

import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.plot(range_n_clusters,ssd)
plt.show()

We can see that the elbow curve suggests a value of k = 4.

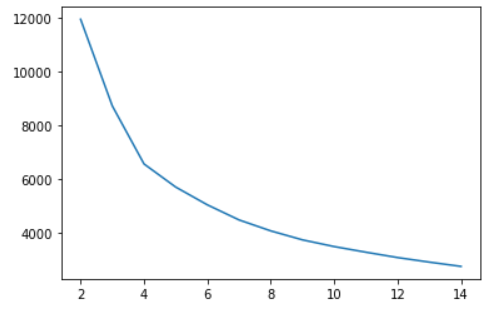
Note: When I tried my model for k = 4 then I could not form much differences in the clusters in terms of business story. But on using k = 3, I could make business sense out of the clusters. Thus, elbow curve is one of the approaches to reach out for the best value of 'k', however, we should also be able to make business sense out of the created clusters. Thus we will build our final model with k = 3.

kmeans = KMeans(n_clusters=3, max_iter=50)
kmeans.fit(X_scaled)
 kmeans.labels_

Output: array([2, 1, 0, ..., 2, 0, 0])

We are now saving the cluster labels in our original dataset to understand our business sense:

X['Cluster_Id'] = kmeans.labels_
X.head()

Let us visualise the clusters by each variable.

import seaborn as sns

Box plot to visualise Cluster Id vs Amount: In the below boxplot we can see that customers in cluster ID 1 have high transaction amount, while cluster ID 2 have low transactional amount.

sns.boxplot(x='Cluster_Id', y='Amount', data=X)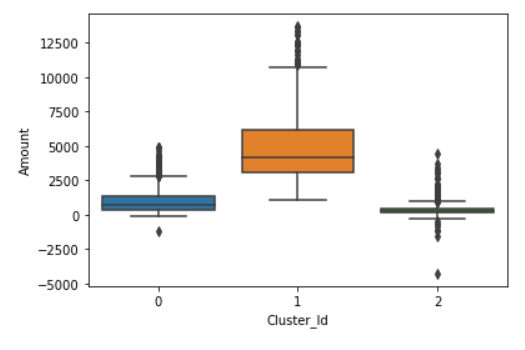

Box plot to visualize Cluster Id vs Frequency. It can be noticed that customers in cluster ID 1 have high frequency while cluster ID 2 do not come that frequently.

sns.boxplot(x='Cluster_Id', y='Frequency', data=X)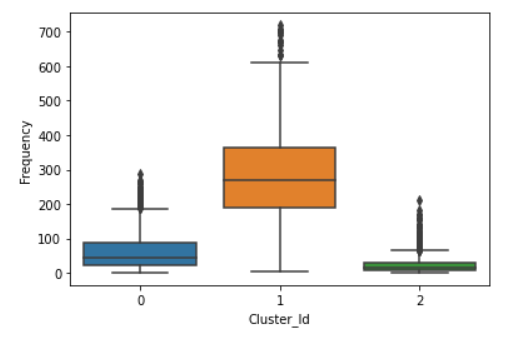

Box plot to visualize Cluster Id vs Recency: Customers in cluster ID 3 have high recency i.e., they have come long ago while cluster ID 1 have low recency, indicating they have come more recently into the store.

sns.boxplot(x='Cluster_Id', y='Recency', data=X)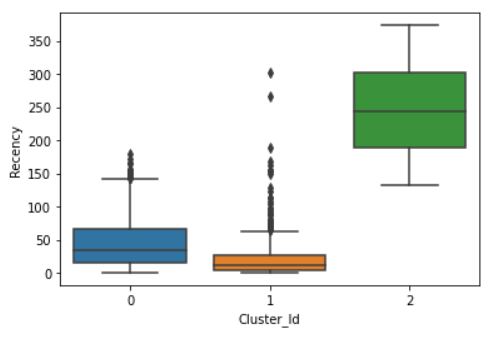

Final Conclusion:

Customers with Cluster Id 1 are the customers with high amount of transactions, come more frequently and have recently come to the store as compared to other customers. They are our loyal customers.

Customers with Cluster Id 2 are not recent buyers, have low frequency and have come long ago in our store and hence least of importance from business point of view.